Background Information
The Pre-lab portion of the lab consisted of learning the implementation of Bayes Filter in grid localization. The codebase for the simulation was provided in class and I had to implement the code just for the grid localization of the virtual robot.
The robot state is given as an array of [x, y, theta], defined as the robot's pose. With this, the purpose of the Bayes Filter is to update the belief in the robot (the probability that the robot is in a certain state) using the sensor values. Thus, the Bayes Filter algorithm allows us to predict the robot's position and update its position that reduces its uncertainty.
Code Implementation
Shown below is the Bayes Filter algorithm that we are implementing in this lab, where for every position, we predict the location of the robot and update it accordingly. The algorithm is divided up into several helper functions, each explained below: computer_control(), odom_motion_model(), prediction_step(), sensor_model() and update_step().

Compute Control
The first function, compute_control(cur_pose, prev_pose), takes in two parameters -- current and previous pose and returns the necessary variables for the Bayes Filter algorithm. It returns delta_rot_1, delta_trans, delta_rot_2, which are the two rotation one translation values between the two poses.
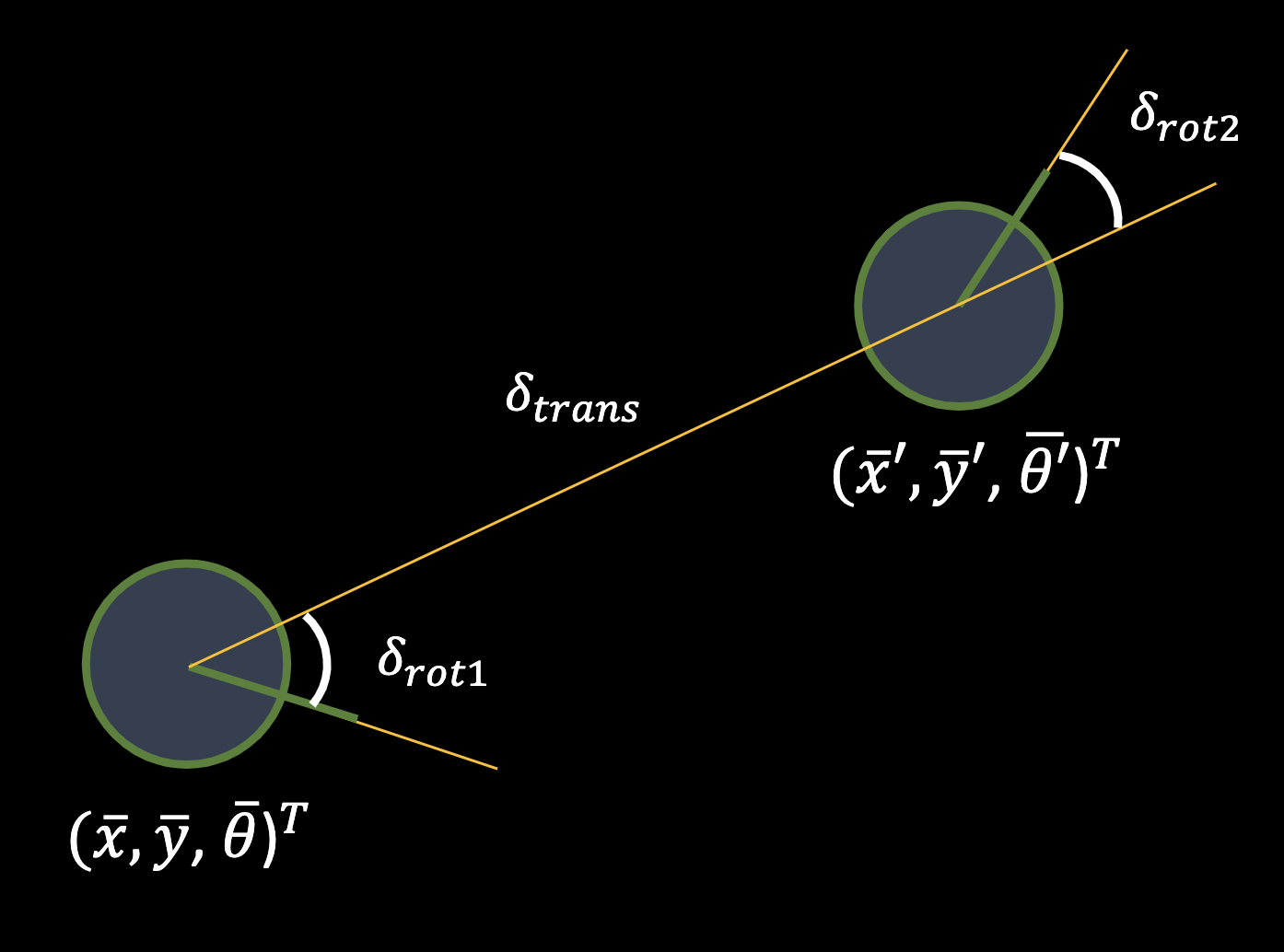
Using trignometry and python math/np, I calculated the angle between the current heading and translation angle (delta_rot_1), the translation distance (delta_trans), and the angle between the translation angle and final heading (delta_rot_2).
Below is the code snippet of this function.

Odometry Motion Model
Next step is to compute the probability that the robot would end up in the current pose, given a control input and previous pose. We used the gaussian function and multiplied the probability of (rot1, trans, rot2) to get the final odometry motion probability.

The code implementation is as follows.

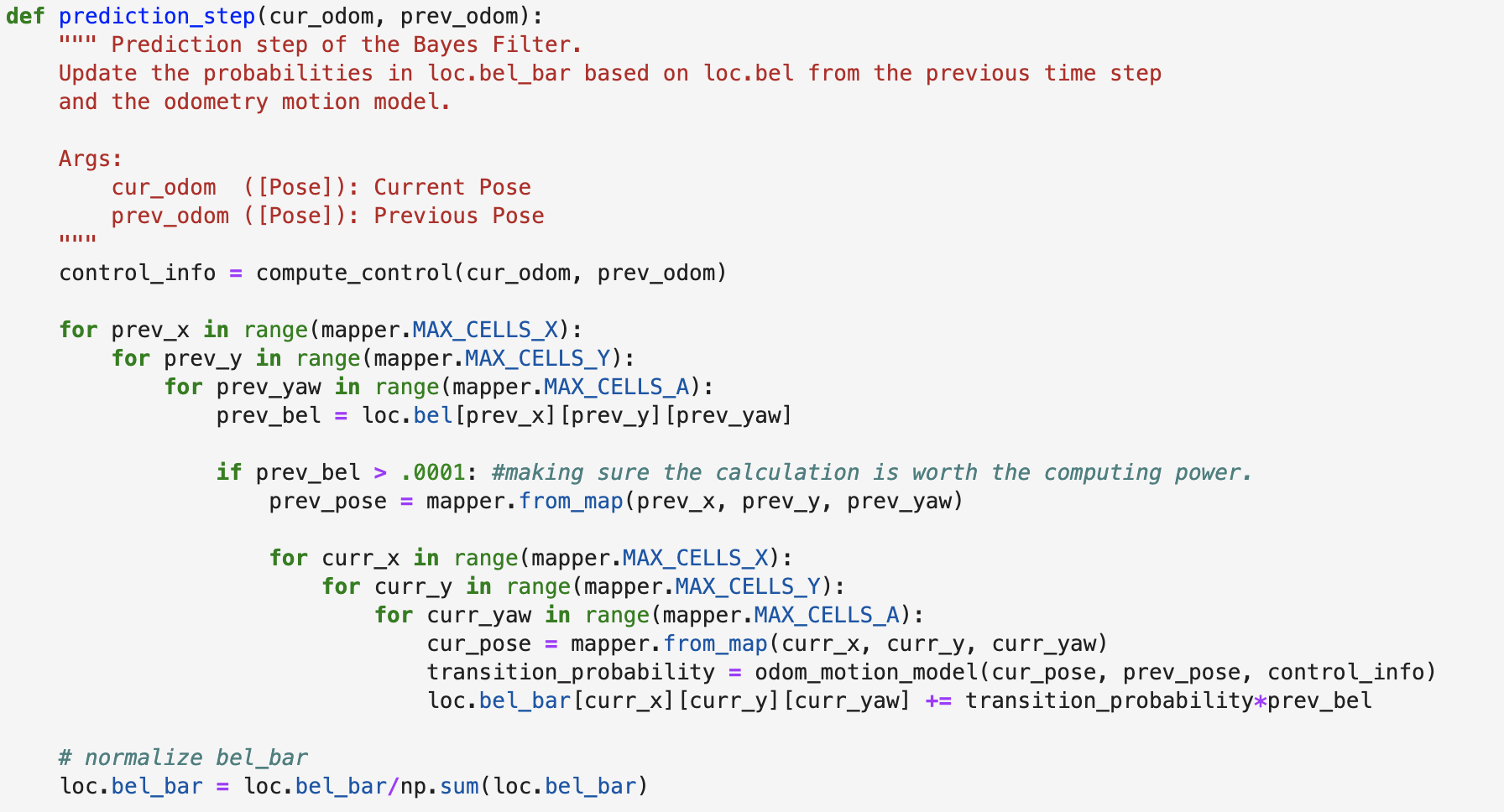
Prediction Step
The prediction step utilized the current and previous position of the robot to create the belief_bar in the algorithm. I used six nested for loops: first three for the previous pose and the last three for current pose. The function calculated the probability of getting from the previous position to the current position and multiplied it with the belief in the previous step. After summing that value for each position, it was stored in loc.bel_bar after normalizing the sum.
The code implemention is as follows.
Sensor Model
Now that the prediction step is over, it is time to update the robot's position. This step uses the gaussian function once again, like the motion model, but for the sensor output values. It computes the likelihood of getting accurate sensor readings given the robot's pose. With the given sigma value, I looped through the 18 sensor measurements and calculated the probability that the sensor readings are accurate. Then, the 18 probability values are appended to thr prob array and later multiplied all together in update_step().
The implemented code is shown below.

Update Step
With three nested-loops, I iterated through every possible current poses of the virtual robot and multiplied the intermediate belief (output of the prediction step) with the sensor readings probability from sensor model. Then I updated the belief at each pose with the multiplied value. After the for loops are over, the probability is again normalized and stored in loc.bel.
This is the update_step function.

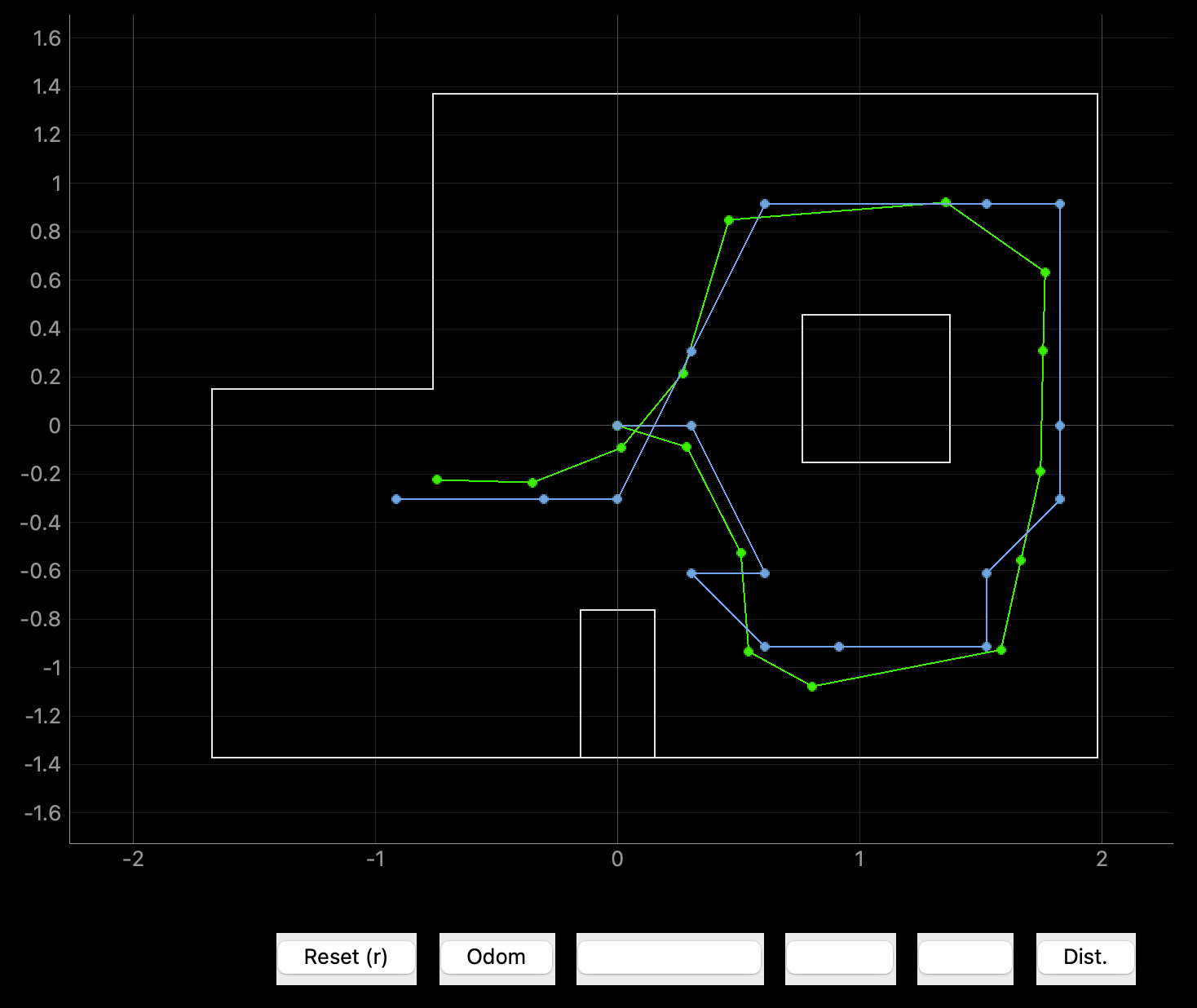
Results
The Bayes filter implementation results are shown below, where green is the true pose and blue is the belief.